�ŋ߂̌����T�v
���w�̕���ł͌��q�E���q�n�Ƃ��Ă̕����̐����ׂ邽�߂ɁA�����I��@�ȊO�ɃR���s���[�^�[�E�V�~�����[�V�����̕��@���L���p�����Ă����B�����́A���̔��e�̒��ŗʎq�����q�E���q�n�̃_�C�i�~�N�X�E�V�~�����[�V�����̕��@�W������Ɠ����ɁA�����ʎq����тт����݂̉��w������ቷ�ł̗ʎq���ہi�ቷ�̉t�́E�����E�N���X�^�[�̃_�C�i�~�N�X�j�։��p���A�����̕����E���ۂ�挱�I�ɉ𖾂��錤�����s���Ă���B
�T�D �ʎq�����q�E���q�n�_�C�i�~�N�X�E�V�~�����[�V�����̓W�J
�������̌��q�E���q�̗ʎq�_�C�i�~�N�X�A����т��ꂪ�N���ƂȂ镨���⌻�ۂ��𖾂��邱�Ƃ́A�Ƃ��ɂQ�P���I�����̉��w�̍ł��傫�ȉۑ�̈�ł���B�����͑����̌��q�E���q���琬��u�����q�E���q�n�v�ł��邪�A���̌��q�E���q�̃_�C�i�~�N�X���V�~�����[�V�����ŒT����@�͏]���A�ÓT�͊w�Ɋ�Â������q���͊w�iMD�j�V�~�����[�V��������ł������B���̂悤�ȌÓT�IMD�V�~�����[�V�����́A���ɓ��v�͊w�I�ɐ����ȕ��@���m������Ċe��̑̌n�ɕՂ����p����A���͂⊮���̈�ɂ���B����������A���q�E���q���y���ĉ��x���Ⴍ�A���̉^�����ÓT�͊w�����E���ėʎq���ʂ������ꍇ�A���̌��q�E���q�́u�ʎq�_�C�i�~�N�X�i�ʎq���ʂ��܂ރ_�C�i�~�N�X�j�v���V�~�����[�V�����ŒǐՂ��邱�Ƃ́A���݂̍ł���[�I�Ȍ����ۑ�ł���B�����I�ɂ͎��Ԉˑ��̃V�����f�B���K�[�������𐔒l�I�ɉ����悢�̂ł��邪�A���̕������͂S���q���x�ȏ�̑����R�x�̑̌n�ɂȂ�ƌ��݂̃R���s���[�^�[�̔\�͂ł͉����Ȃ��Ȃ邽�߁A�������̌��q�E���q�̗ʎq�_�C�i�~�N�X�̗����͗e�Ղɂ͐i�W���Ȃ������B
�������A1994�N��Cao��Voth�� J. Chem. Phys. �ɔ��\�����u�a�H�ϕ��Z���g���C�h���q���͊w�i�b�l�c�j�@�v�Ȃ����I�Ȍv�Z�@��p����A���̕ǂ�ł��j�邱�Ƃ��ł���B���Ȃ킿�A CMD�͋ߎ��I�ɂł͂��邪���̔M�͊w�I�����i���鉷�x�A���鈳�́j���ł̑����̗ʎq���q�̃_�C�i�~�N�X���V�~�����[�g�ł���B����͕s�m�萫�����ɗR������ʎq���U�̌��ʂ��a�H�ϕ��@�ɂ���Ď������ꂽ���̔��ÓT�ߎ��Ɋ�Â����@�ł���B���̃V�~�����[�V��������ʎq���v�͊w�I�����ԑ��֊��i�I�u�U�[�o�u���j�A���Ȃ킿�ʎq�_�C�i�~�N�X���v�Z�ł��邱�Ƃ��m���Ă���B
������Cao��̔��\�̗��N�ȍ~�A���̂b�l�c�̌v�Z�Z�@�i�A���S���Y���j�E�\�t�g�E�F�A�𐢊E�ɐ�삯�ĊJ�����A��Ƃ��ăp�����f�n�̗ʎq�_�C�i�~�N�X���V�~�����[�g���Ă����i�_��7,8�j�B���݂ł��܂�CMD�ȊO�ɂ͗ʎq�����q�E���q�n�̗ʎq�_�C�i�~�N�X���v�Z�ł�����@�͑��݂��Ă��Ȃ��B�܂��ACMD���h���C�u���Ă��錤���O���[�v�͂������܂߂Đ��E��3�`4�O���[�v���x�������Ȃ��B
�U�D �t�̐��f�̏W�c��N��CMD�ɂ��挱�I�\��
�ÓT�t�̂Ɠ������A�ʎq�t�̂ɂ����Ă��W�c��N�\�\�����Ԕ͈͂ł̌��q�E���q�̃O���[�v�̏W�c�I�ȉ^���\�\�����݂���B���̏W�c�I�^���͎����I�ɂ͒����q��e���U���ɂ���Ċϑ�����邪�A����܂Ŏ����̍���̂��߂ɉt�̃p�����f�ɑ��ẮA�B��1973�N�̔�e���U���������s�����Ȍ��ʂ���Ă����ɉ߂��Ȃ��B�]���āA���f�͂����Ƃ���{�I�ȕ����ł���̂ɂ�������炸�A���̕����̉t�̏�ԂŋN�����Ă��镪�q�̏W�c�I�ȉ^���ɂ��Ă͂悭�킩���Ă��Ȃ������B������1998�N�ɂb�l�c�V�~�����[�V�����ɂ���āA�t�̃p�����f�̓��I�\�����q S(k,��)���v�Z�����i�_���U�j�B����̓R���s���[�^�[�E�V�~�����[�V������ʂ̂����ŁA�ʎq�t�̂̏W�c�^���Ɋւ��鐢�E���̌v�Z�ł��������A���̌v�Z���ʂ͂��̗��N�i1999�N�j���B�ŋ��͂Ȓ����q����p���čs��ꂽ��e���U�������ɂ���Ċϑ��A�ǔF���ꂽ�i���̎������ʂ�1973�N�̎������ʂ���������CMD�̕��ɂ悭��v���Ă����B���}�Q�ƁB�_��2,3�j�B������̗ʎq�t�̂̏W�c��N�͌ÓTMD�ł͑S���L�q�ł����A���q�̗ʎq�����W�c��N�̗v���ł��邱�Ƃ����炩�ɂȂ����B�����̂���CMD�v�Z�͎������ʂ��P�N�O�ɗ\�����Ă������ƂɂȂ�B
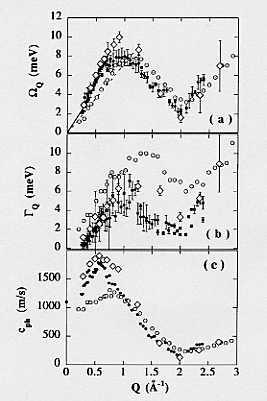
�}�D �t�̃p�����f�̏W�c��N�p�����[�^�[.
(a) ��N�G�l���M�[; (b) �����萔; (c) �ʑ����x.
��,�� �����q����; �� CMD; �� �ÓTMD.
�����q������CMD�Ƃ̈�v�͂悢�B�ÓTMD�͑S�������q�������ʂ��Č����Ă��Ȃ��B
�V�D �{�[�Y���v����уt�F���~���v�ɏ]���ʎq�����q�E���q�n�_�C�i�~�N�X�v�Z�@�̊J��
Cao-Voth�̂b�l�c�@�̓{���c�}�����v�ɑ�����̂ł��邪�A�ቷ�ł͗Ⴆ�Ήt�̃w���E���S�Ɍ�����悤�ɁA�̌n�̓{���c�}�����v�����E���{�[�Y/�t�F���~���v�̌��ʂ������ɂȂ�B���̌��ʁA�������A�{�[�Y�|�A�C���V���^�C���Ïk�̂悤�ȓ��قȗʎq���ۂ���������B�����̌��ۂ͉��w�̕���ł��ߔN���q���������Ȃǂő傫�Ȓ��ڂ��W�߂Ă���A�{�[�Y/�t�F���~�����q�E���q�n�̗ʎq�_�C�i�~�N�X�̂��߂̃V�~�����[�V�����̊J�����ؖ]����Ă����B1999�N�ɂ����͂b�l�c�@���{�[�Y/�t�F���~���v�Ɋg�����邱�Ƃɐ������A���̌��ʗʎq���q�̗ʎq���U�̌��ʂ����łȂ����v�I���ւ̌��ʂ�����荞�A�ʎq�_�C�i�~�N�X�E�V�~�����[�V�����̕��@���J�������i�g�{�[�Y/�t�F���~CMD�h�A�_��2,4,5�j�B����ɍŋ߁A���̊g��������@����m���ɗʎq���v�͊w�I�I�u�U�[�o�u���Ƃ��Ă̎��ԑ��֊����v�Z�ł��邱�Ƃ���͓I�ɏؖ������i�_��1�j�B���̂����̌��_�͂��̌�Blinov-Roy-Voth�ɂ���Ă��Ǐؖ�����A�����̊J�������X�L�[���������ł��邱�Ƃ��m�F���ꂽ�B�g�{�[�Y/�t�F���~CMD�h�́A�{�[�Y/�t�F���~�����q�E���q�n�̗ʎq�_�C�i�~�N�X���V�~�����[�V�����Ōv�Z�ł���L�͂ȕ��@�ł��邾���łȂ��AMD�V�~�����[�V�����̎�@���Ɍ��܂Ŋg���������̂ł���A�R���s���[�^�[�E�V�~�����[�V�����̒������u���[�N�X���[�ł���Ǝ������Ă���B
��v���\�_���F
1. K. Kinugawa, H. Nagao, and K. Ohta, "A semiclassical approach to the dynamics of many-body Bose/Fermi
systems by the path integral centroid molecular dynamics", J. Chem. Phys. 114, 1454-1466 (2001).
2. K. Kinugawa, H. Nagao, and K.Ohta, "A path integral centroid molecular dynamics method for Bose and
Fermi statistics," J. Mol. Liquids (Special Issue) 90 , 11-20 (2001).
3. F.J. Bermejo, K. Kinugawa , C. Cabrillo, S.M. Bennington, B. Fåk, M.T. Fernández-Díaz, P. Verkerk, J.
Dawidowski, and R. Fernández-Perea, "Quantum effects on liquid dynamics as evidenced by the presence of
well-defined collective excitations in liquid para-hydrogen," Phys. Rev. Lett. 84, 5359-5362 (2000).
4. K. Kinugawa, H. Nagao, and K. Ohta, " Path integral centroid molecular dynamics simulation extended to
Bose and Fermi statistics: method and applications," Prog. Theor. Phys. Suppl. 138 , 531-532 (2000).
5. K. Kinugawa, H. Nagao, and K. Ohta, "Path integral centroid molecular dynamics method for Bose and Fermi
statistics: formalism and simulation," Chem. Phys. Lett. 307, 187-197 (1999).
6. K. Kinugawa, "Path integral centroid molecular dynamics study of the dynamic structure factors of liquid
para-hydrogen," Chem. Phys. Lett. 292, 454-460 (1998).
7. K. Kinugawa, P.B. Moore, and M.L. Klein, "Centroid path integral molecular-dynamics studies of a
para-hydrogen slab containing a lithium impurity," J. Chem. Phys. 109, 610-617 (1998).
8. K. Kinugawa, P.B. Moore, and M.L. Klein, "Centroid path integral molecular dynamics simulation of lithium
para-hydrogen clusters," J. Chem. Phys. 106, 1154-1169 (1997).